Algorithm-Dynamic Programming

Posted on | Post modified | In |

Algorithm-Dynamic Programming

  • Divide-and-Conquer： 子問題彼此獨立、不重複
  • Dynamic Programming： 子問題會重複出現，要記下來避免重算
  • 使用DP的時機: 線性的排序法 + 無法重新排列
    • Optimal Substructure: 整體最佳解可以由子問題的最佳解組合而成
    • Overlapping Subproblem: 同一個子問題會被反覆計算很多次 </span>
  • 常見例子
    • Linear assembly lines
    • matrices in a chain
    • characters in a string
    • points around the boundary of a polygon
    • points on a line/circle
    • the left to right order of leaves in a search tree
    • …
  • 在DP問題中，subproblem的最佳解不見得是overall的最佳解
  • DP問題可以直接畫表格的方式，用簡單的計算就知道哪一個solution是optimal(Tabular Method)
面向 Divide-and-Conquer Dynamic Programming
子問題關係 彼此獨立 大量重疊
是否記憶結果 ❌ 不需要 ✅ 必須（memo / table）
典型技術 Recursion Recursion + Memoization 或 Iteration
時間優化關鍵 問題切得平均 避免重複計算
思考重點 怎麼「分」 狀態如何「轉移」

Assembly-line Scheduling

  • Shortest Path Algorithm也是需要DP的觀念
  • 只要記得最短路徑這個最佳解就好，其他路徑不重要

車子組裝生產線例子

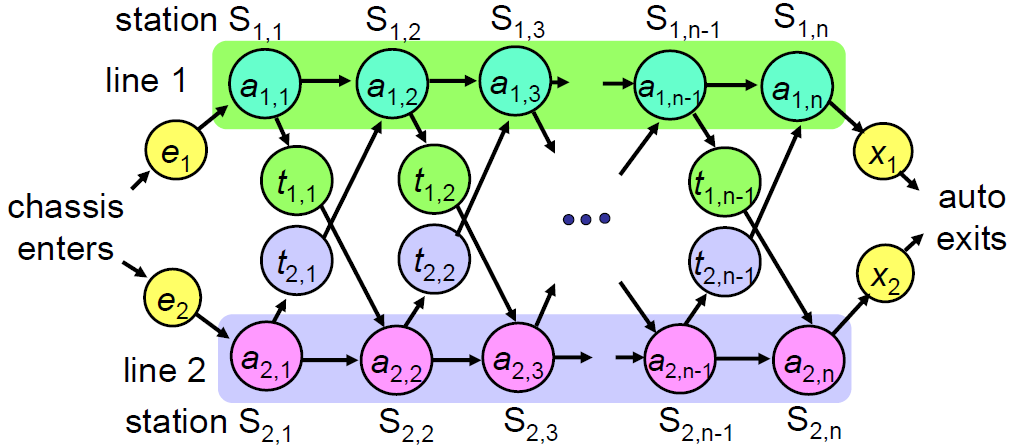
  • Objective: 在例子中，找一個生產線的走法，使時間成本更少
    • 可以轉換生產線，但要付出時間成本$t_{i,j}$ → $i$代表生產線，$j$代表需要的station
  • Worst Case: $\Omega (2^n)$: 暴力法

解法

  • 先找到Optimal Sustructure 要找到$S_{1,n}$之前的最佳解，需要從入口到$S_{1,n-1}$之前的最佳解，把之前的路徑用divide and conquer解就可以了。
  • 先找到Overlapping Subproblem
    • $f_i[j]$代表從起點到$S_{i,j}$最短的時間，目前先考慮第一條生產線，如果$j$只有一個那就只有一種走法；大於兩條之後，可以考慮換生產線，當然要加上轉換的時間，這個是用table的方式呈現，分別紀錄$f_{1,1},f_{1,2},f_{1,3},…,f_{1,n}$和$f_{2,1},f_{2,2},f_{2,3},…,f_{2,n}$分別是多少，以本例子來說是一個2*n的table size
    \[f_i[j] = \left\{ \begin{array}{l} e_1 + a_{1,1}, \text{if}\ j = 1 \\ min(f_1[j-1] + a_1,j,f_2[j-1] + t_{2,j-1} + a_{1,j}), \text{if}\ j \ge 2 \end{array} \right.\]
  • 實際的Pseudo Code
    • 仔細看pseudo code還蠻簡單的，就只是實作出前面寫的formula而已
    • asterisk symbol代表optimal solution
    • 前面的$f$已經紀錄到$S_{i,j}$的最短路徑是多少，可是到底是從哪一條生產線來的不知道，所以需要另外一個table來紀錄，這就是$I$這個table存在的目的，大小是x*(n-1)

Matrix-chain subsequence (矩陣相乘以及相乘的順序)

  • $A$是pxq matrix；$B$是qxr matrix；$C=AB$是pxr: $C[i,j]=\sum\limits_{k = 1}^q{A[i,k]B[k,j]}$
  • Time Complexity: $O(pqr)$
1
2
3
4
5
6
7
8
9
10
Matrix-Multiply(A, B)
if A.columns ≠ B.rows
    error "incompatible dimensions" // 先檢查相乘的矩陣維度是否valid
else let C be a new A.rows * B.columns matrix
    for i = 1 to A.rows
        for j = 1 to B.columns
            c_ij = 0
            for k = 1 to A.columns
                c_ij = c_ij + a_ik * b_kj
    return C

3個矩陣以上就會有順序的問題

  • Objective: 使乘法數量越少越好
  • 例子: $A_1$: 4x2;$A_1$: 2x6;$A_3$: 5x1
    • $(A_1A_2)A_3$: 4*2*5+4*5*1=60
    • $A_1(A_2A_3)$: 2*5*1+4*2*1=18
  • 問題: 要怎麼知道一個Matrix-Chain怎麼乘會讓乘法的operations數量最少?

    • BruteForce: $P(n)$代表$n$個矩陣相乘的方法有多少種，$\Omega({4^n\over {n^{3/2}}})$

      \[P(n) = \left\{ \begin{array}{l} 1, \text{if}\ n = 1 \\ \sum\limits_{k=1}^{n-1}{P(k)P(n-k)}, \text{if}\ n \ge 2 \end{array} \right.\]
  • 先判斷能不能用DP
    • 因為matrix chain是linearly ordered並且不能rearranged(每一種矩陣都要存在並且順序不能被改變)
    • Optimal Substructure:如果最優解在第 $k$ 個位置切開，那麼左半部$A_i,…A_k$，右半部$A_{k+1},…,A_j$都一定各自是最優的，否則：如果左邊不是最優，換成更好的左邊，整體一定更好（矛盾）
    • Overlapping Subproblem: 子問題是什麼？$m[i][j]$計算$A_i,…,A_j$代表最小成本，當計算$m[1][4]$和$m[2][5]$，都會用到$m[2][4]$
\[m[i,j] = \left\{ \begin{array}{l} 0, \text{if}\ i = j \\ \min\limits_{i\le k\lt j}\{m[i,k] + m[k+1, j] + p_{i-1}p_kp_j\}, \text{if}\ i \lt j \end{array} \right.\]

利用DP解決-Iterative Bottom-Up

這也很簡單，只要自己推過一層就會了，也是有兩個table一個記錄矩陣相乘的operations數量，另外一層則紀錄從哪裡切會是最小值。屬於bottom-up的想法

  • 一開始先計算$A_1A_2$,$A_2A_3$,…,$A_{n-1}A_n$共$n-1$各是多少
  • 然後計算$A_1A_2A_3$,$A_2A_3A-4$,…,$A_{n-2}A_{n-1}A_n$共$n-2$各是多少
  • 以此類推就可以建立上述的兩個table，個人認為是比較聰明的brute force

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Matrix-Chain Order(p)
n = p.length - 1
Let m[1..n, 1..n] and s[1..n-1, 2..n] be new tables
for i = 1 to n
    m[i,i] = 0
for l = 2 to n // l is the chain length
    for i = 1 to n - l + 1
        j = i + l - 1
        m[i,j] = ∞
        for k = i to j - 1
            q = m[i,k] + m[k+1, j] + p_[i-1] * p_[k] * p_[j]
            if q < m[i,j]
                m[i,j] = q
                s[i,j] = k
return m and s

1
2
3
4
5
6
7
Print-Optimal-Parens(s, i, j)
if i == j
    print “A-i”
else print “(“
    Print-Optimal-Parens(s, i, s[i, j])
    Print-Optimal-Parens(s, s[i, j] + 1, j)
    Print “)“

利用DP解決-Top-Down Recursive Matrix-Chain Order(不推薦)

  • 使用這個邏輯解題會有很多問題被重複解，很浪費時間，DP還是建議用bottom-up
  • Time: $\Omega (2^n)$: $\sum\limits_{k=1}^{n-1}(T(k)+T(n-k)+1)$
1
2
3
4
5
6
7
8
9
Recursive-Matrix-Chain(p, i, j)
if i == j
    return 0
m[i, j] = ∞
for k = i to j -1
    q = Recursive-Matrix-Chain(p, i, k) + Recursive-Matrix-Chain(p, k+1, j) + p[i-1]p[k]p[j]
    if q < m[i,j]
        m[i,j] = q
return m[i,j]

利用DP解決-Top-Down Memorization Matrix-Chain Order

  • 把subproblem的解記憶起來就不會發生重複解的問題
  • Space: $O(n^2)$
  • Time: $O(n^3)$
1
2
3
4
5
6
7
Memoized-Matrix-Chain(p) // p = <p0, p1, .., pn>
n = p.length - 1
let m[1..n, 1..n] be a new table
for i = 1 to n
    for j = i to n
        m[i, j] = ∞
return Lookup-Chain(m, p,

1
2
3
4
5
6
7
8
9
10
Lookup-Chain(m, p, i, j)
if m[i, j] < ∞
    return m[i, j]
if i == j
    m[ i, j] = 0
else for k = i to j -1
    q = Lookup-Chain(m, p, i, k) + Lookup-Chain(m, p, k+1, j) + pi-1pkpj
    if q < m[i, j]
        m[i, j] = q
return m[i, j]

Longest Common Subsequence

DNA比對例子

  • Input: $X_m=<x_1,x_2,…,x_m>$, $Y_n=<y_1,y_2,…,y_n>$
  • Output: $Z_k=<z_1,z_2,…,z_k>$: LCS of $X_m$ and $Y_n$

先判斷能不能用DP

  • Optimal Substructure:
    • Case 1: $x_m=y_n$代表兩個sequence的最後一個element是一樣就可以直接放到$Z$中，並且繼續往前比對$X_{m-1},Y_{n-1}$
    • Case 2: $x_m\ne y_n$代表兩個sequence的最後一個element不一樣
      • Case 2-1: 則$z_k\ne x_m$代表$Z$是$X_{m-1}$和$Y$的LCS
      • Case 2-2: 則$z_k\ne y_n$代表$Z$是$X$和$Y_{n-1}$的LCS

    \(c[i,j] = \left\{ \begin{array}{l} 0, \text{if}\ i = 0\ \text{or}\ j=0 \\ c[i-1,j-1], \text{if}\ x_i = y_i, j\lt 0 \\ \max(c[i,j-1],c[i-1,j], \text{if}\ x_i \ne y_i, j\lt 0 \end{array} \right.\)

    • $c[i,j]$代表$X_i$和$Y_j$的LCS長度
    • 當某一個sequence為零，則LCS一定為零
  • Overlapping Subproblem: LCS(5, 5) 和 LCS(6, 5)都會算 LCS(5, 4) ➡️ 同一個 (i, j) 被重算很多次

利用DP解決-Bottom-Up

  • Time: $O(mn)$就是二維table的大小
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
LCS-Length(X,Y)
m = X.length
n = Y.length
let b[1..m, 1..n] and c[0..m, 0..n] be new tables
for i = 1 to m
    c[i, 0] = 0
for j = 0 to n
    c[0, j] = 0
for i = 1 to m
    for j = 1 to n
        if x[i] == y[j]
            c[i, j] = c[i-1, j-1]+1
            b[i, j] = "↖"
        elseif c[i-1,j] >= c[i, j-1]
            c[i,j] = c[i-1, j]
            b[i, j] = "↑" 
        else
            c[i, j] = c[i, j-1]
            b[i, j] = "←"
return c and b

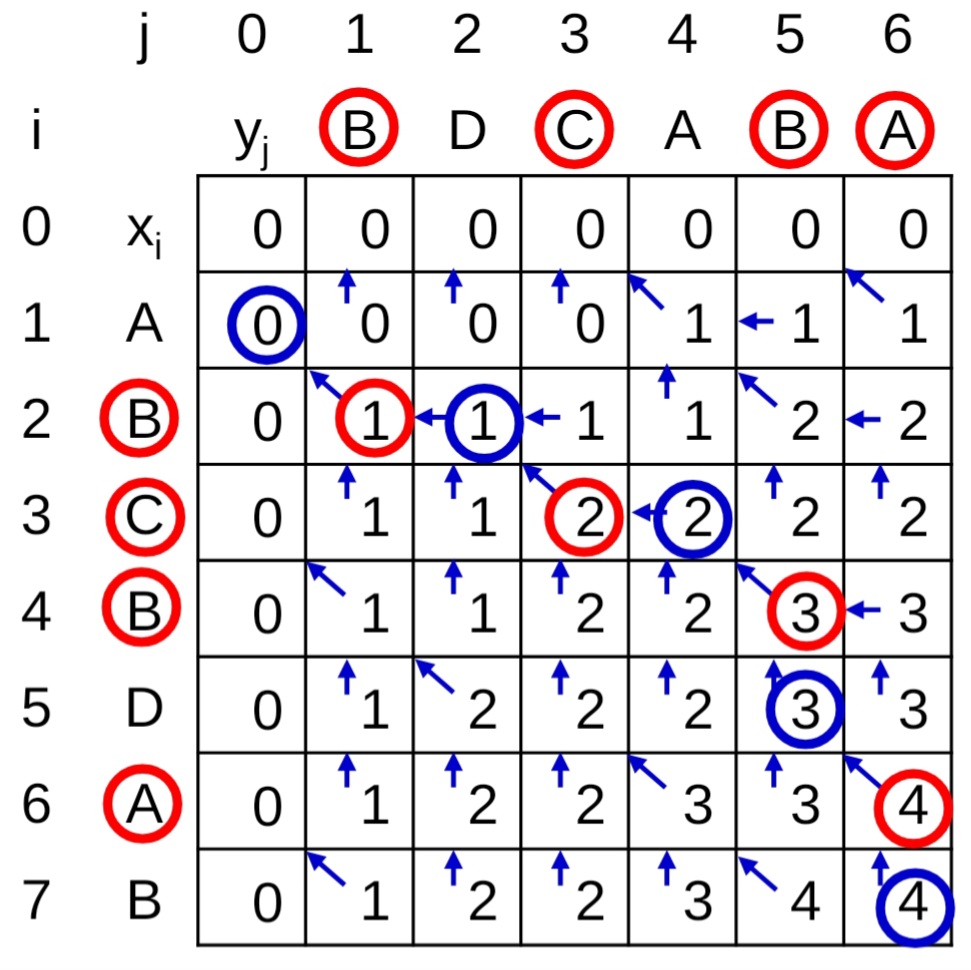
  • Input: $X=<A,B,C,B,D,A,B>, Y=<B,D,C,A,B,A>$
  • Output: $LCS=<B,C,B,A>$
  • 從上到下或從左到右填入
  • 當$A\ne B$，去看$j-1$和$i-1$誰大，兩者都是零就直接填上方的零，箭頭是為了方便trace，只要看到左斜的arrow，就把對應的字母圈起來
1
2
3
4
5
6
7
8
9
Print-LCS(b, X, i, j) // 只是把答案print出來
if i == 0 or j == 0
    return
if b[i, j] == "↖"
    Print-LCS(b, X, i-1, j-1)
    print x[i]
elseif b[i, j] == "↑"
    Print-LCS(b, X, i-1, j)
else Print-LCS(b, X, i, j-1)

Optimal binary search trees

  • Input:
    • $K=<k_1,k_2,…,k_n>$: 給定一個已經sorted的不同的key，可以想像成英文字典的概念
    • 每個key都會有找的到的機率$P=<p_1,p_2,…,p_n>$
    • 而$D=<d_1,d_2,…,d_n>$代表沒有出現在字典的那些key
    • 對於那些沒有在字典的key也會有找不到的機率$Q=<q_1,q_2,…,q_n>$
  • Objected: 找搜尋成本最低的binary search tree
    • 成本計算方式: 算找的到的key的期望值 + 找不到的key的期望值，用深度+1的方式當作成本
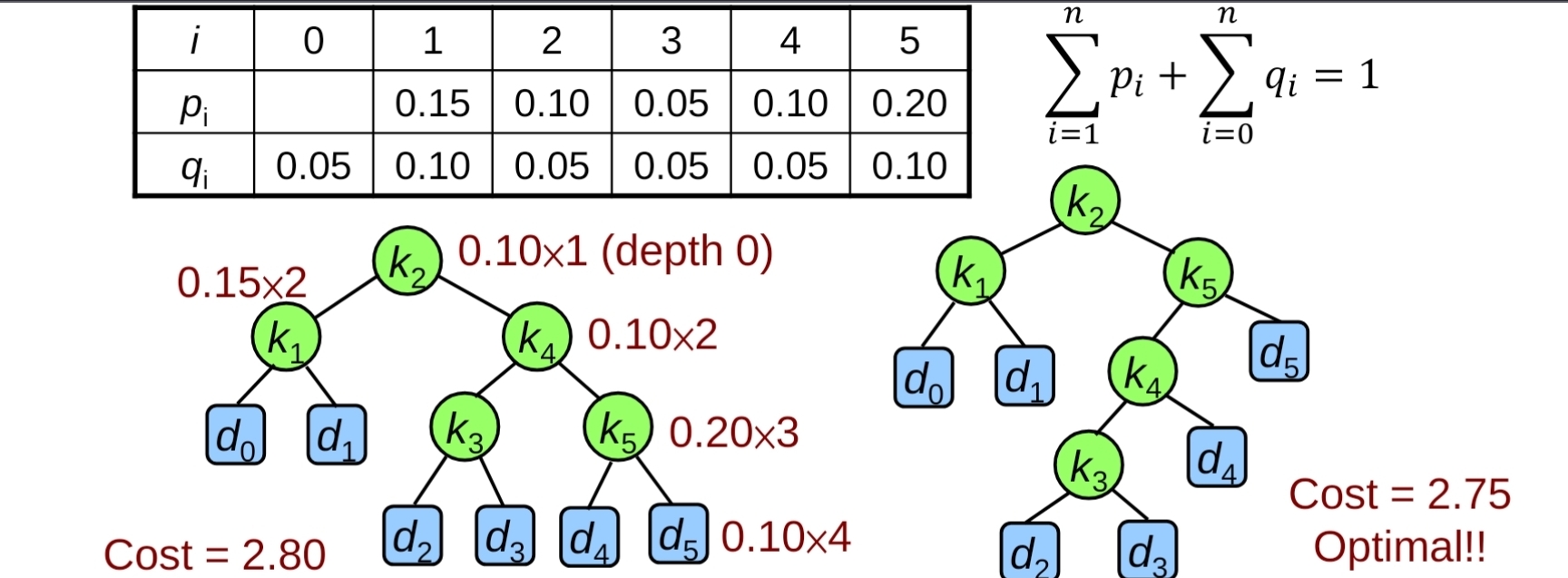
    \[E[\text{search cost in }T]=\sum\limits_{i=1}^n (\text{depth}_T(k_i)+1*p_i+\sum\limits_{i=0}^n (\text{depth}_T(d_i)+1*q_i\]

利用DP解決-Recurrence

  • Optimal Substructure: 核心邏輯是如果BST $T$有一個subtree $T’=<k_i,…,k_j>$，則這個$T’$對於$k_i,…,k_j,d_{i-1},…,d_j$也一定要是optimal，所以其實和之前的DP問題一樣，例如Matrix-chain subsequence，都是用金字塔表格，假設在最優解中，區間 $[i,j]$中 的 root 是 $k_r$，那麼一定滿足：左子樹 $[i,r-1]$ 是 最佳的；右子樹 $[r+1,j]$ 是 最佳的，如果左子樹不是最佳，換成更好的左子樹，整體期望成本一定更小（矛盾）
  • Overlapping Subproblem: 在計算不同區間時，會反覆用到同一個子區間，例如 E[2][4] 會出現在 E[1][4]（root = 1）、E[2][5]（root = 5）

總共需要4個table

  • 原本儲存找的到和找不到key的機率$P,Q$

  • $w[i,j]$: 表示「子問題區間 i 到 j 的所有搜尋機率總和」，用來快速計算期望成本，避免之後要用到還要重複計算，增加DP的效率

    \(w[i,j] = \left\{ \begin{array}{l} q_{i-1}, \text{if}\ j = i-1 \\ w[i,j-1]+p_j+q_j, \text{if}\ i\lt j \end{array} \right.\) 也就是：

    • 區間內 所有成功搜尋機率
    • 加上 夾在中間的所有失敗搜尋機率

  • $e[i,j]: $代表$k_i$到$k_j$的optimal binary search tree的期望值(預期搜尋成本)

    \[e[i,j] = \left\{ \begin{array}{l} q_{i-1}, \text{if}\ j = i-1 \\ \min\limits_{i\le r\le j}\{e[i,j-1]+e[r+1,j]+w(i,j)\}, \text{if}\ i\lt j \end{array} \right.\]
  • $root[i,j]$: 代表在$k_i,…,k_j$中有一個$k_r$最適合當作root達到optimal，也就是紀錄optimal solution怎麼來的
  • Objective: 要慢慢推導到$e[1,n]$

Pseudo Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Optimal-BST(p, q, n)
let e[1..n+1, 0..n], w[1..n+1, 0..n], and root[1..n, 1..n] be new tables
for i = 1 to n + 1
    e[i, i-1] = q[i-1]
    w[i, i-1] = q[i-1]
for l = 1 to n
    for i = 1 to n – l + 1
        j = i + l -1
        e[i, j] = ∞
        w[i, j] = w[i, j-1] + pj + qj
        for r = i to j
            t = e[i, r-1] + e[r+1, j] + w[i, j]
            if t < e[i, j]
                e[i, j] = t
                root[i, j] = r
return e and root

反正就是按照table分別填入$w,e,root$，最後只要看root table就可以知道OBST的結構長怎樣

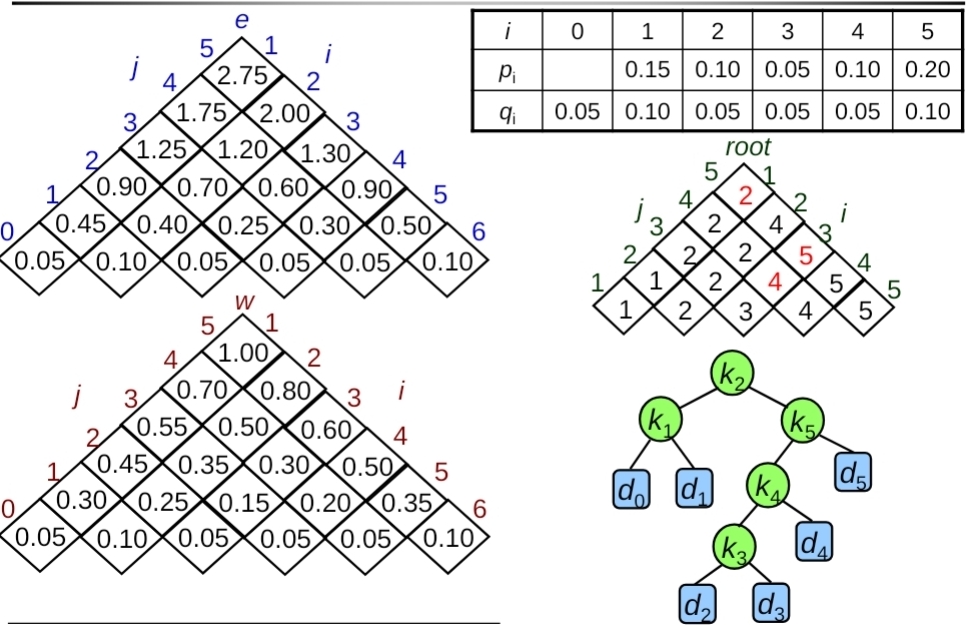
從root[1,5]開始看，是2代表$k_2$當作$[1,5]$的root，左半邊是$k_1$，右邊是$[3,5]$，那就繼續看，發現是5，代表$k_5$當root，依此類推，就可以得出所有root