Algorithm-Sorting

Posted on | Post modified | In |

Algorithm-Sorting

Sorting

  • Comparison-based sorters: 意思是演算法唯一的運算就只有比較兩個數值
    • Merge/Heap接近最佳解
Algorithm Best Case Avg. Case Worst Case In-place Stable
Insertion $O(n)$ $O(n^2)$ $O(n^2)$ Yes Yes
Merge $O(nlgn)$ $O(nlgn)$ $O(nlgn)$ No Yes
Heap $O(nlgn)$ $O(nlgn)$ $O(nlgn)$ Yes No
Quicksort $O(nlgn)$ $O(nlgn)$ $O(n^2)$ Yes No
  • None-Comparison-based sorters: 意思是除了比較數值之外，還會做其他的操作
Algorithm Best Case Avg. Case Worst Case In-place Stable
Counting $O(n+k)$ $O(n+k)$ $O(n+k)$ No Yes
Radix $O(d(n+k’))$ $O(d(n+k’))$ $O(d(n+k’))$ No Yes
Bucket - $O(n)$ - No Yes

Insertion sort

  • Input: 亂序的sequence
  • Output: 正序的sequence
  • Worst Case: Linear $\to T(n) = n^2 \to$ input原本就是reverse sorted order
  • Best Case: Quadratic $\to T(n) = n \to$ input原本就是sorted order

可以想像成把sequence分成兩邊，左邊是已經排序好的，右邊是正要排序，第一個element預設已經排序好，所以從第二個element開始，先把要排序的element保留住(key)，並且左邊所有element只要比key還大就往右邊移動，這樣就可以把key放在正確的位置

1
2
3
4
5
 
InsertionSort(A)
for j = 2 to A.length do
    key = A[j]
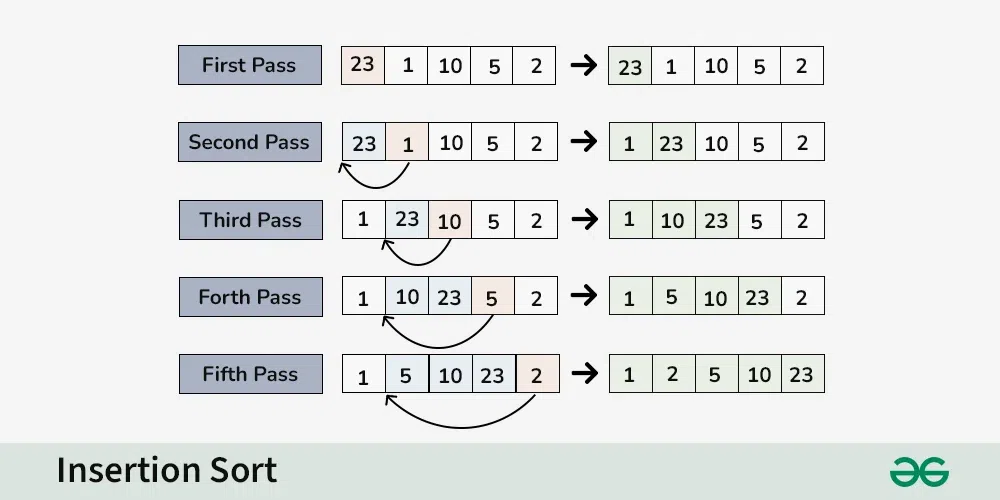
    I =j - 1

Merge Sort

  • Worst Case: $T(n)=O(nlgn)$

是一種divide-and-conquer的演算法，實作會採用recursive的方式，另外，如果$n$足夠大，就會比Insertion Sort還要好。概念也很簡單，一個unsorted sequence 就切一半，切完的兩半各自再切一半，不斷地切直到各自只有≤2的時候，就開始比較誰大誰小並整合起來

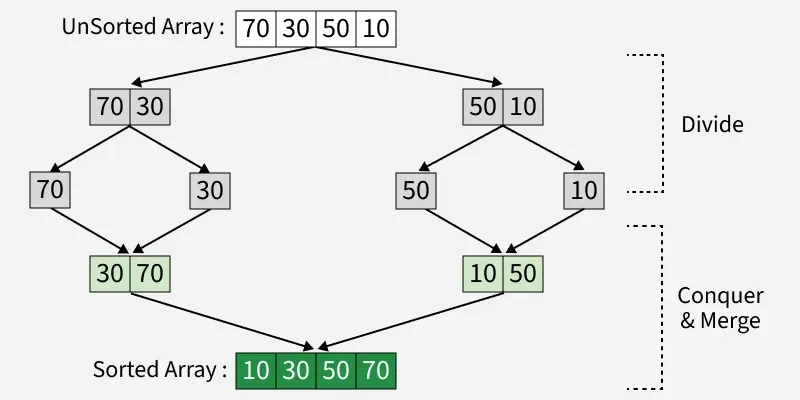
Divide-and-conquer 類型的問題常常可以分解成下面標準的形式

  • $a$代表subproblem的數量
  • $n\over b$代表subproblem的size
  • $D(n)$代表divide n problem into subproble所花的時間
  • $C(n)$代表combine subproblem solution所花的時間
\[T(n)=\left\{ \begin{array}{r} \theta (1), \text{if $n$ \le c}\ aT(n\over b)+D(n)+C(n), \text{otherwise} \end{array} \right.\]

Heap Sort

利用Max-Heap的資料結構實現sorting

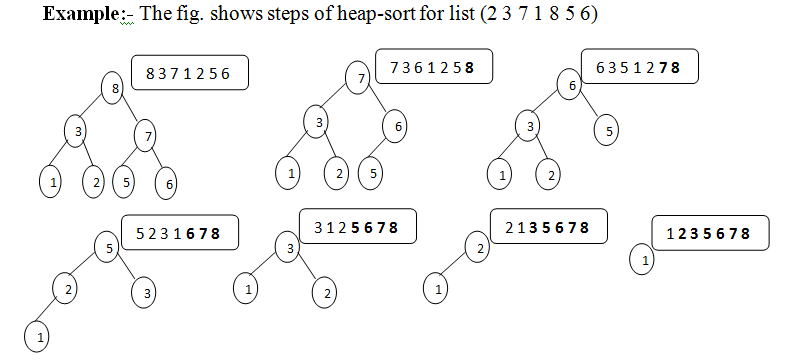
1
2
3
4
5
6
 
HEAPSORT(A)
BUILD-MAX-HEAP(A) // O(n)先建立一個valid max-heap
for i = A.length downto 2
    exchange A[1] with A[i] // O(1)
    A.heap-size = A.heap-size - 1 // O(1)
    MAX-HEAPIFY(A,1) // O(lgn)這個就是實際建置valid max-heap的演算法，也就是符合root比leaf大

Quicksort

  • 有很多種版本，比Heapsort再快一點，同時是一種divide-and-conquer和recursive的演算法
    • $T(q-p)+T(r-q)+\theta(n)$
  • 想法是先把最後一個element當作標準，從頭開始和standard做比較，比standard小的放左邊，大的放右邊，不需要管大/小那一邊各自的順序，比較完之後再分別比大/小的一邊，重複上面的步驟
  • Best Case: 完美平衡，和standard比較之後，直接是兩半: $T(n/2)+T(n/2)+\theta(n)$
  • Worst Case: 當input array是sorted時 
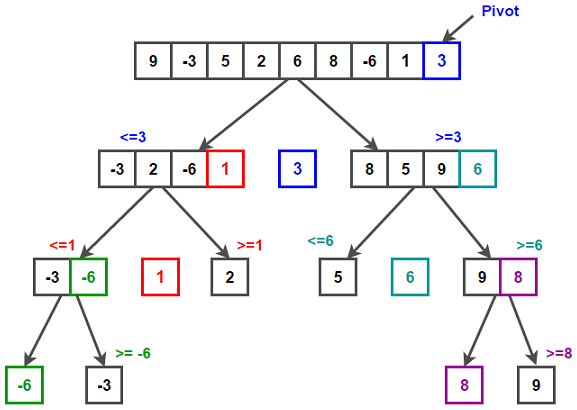
    1
    2
    3
    4
    5
    		 
    QUICKSORT(A,p,r)
if p<r
  q = PARTITION(A, p, r)
  QUICKSORT(A,p,q-1)
  QUICKSORT(A,q+1,r)

Counting Sort

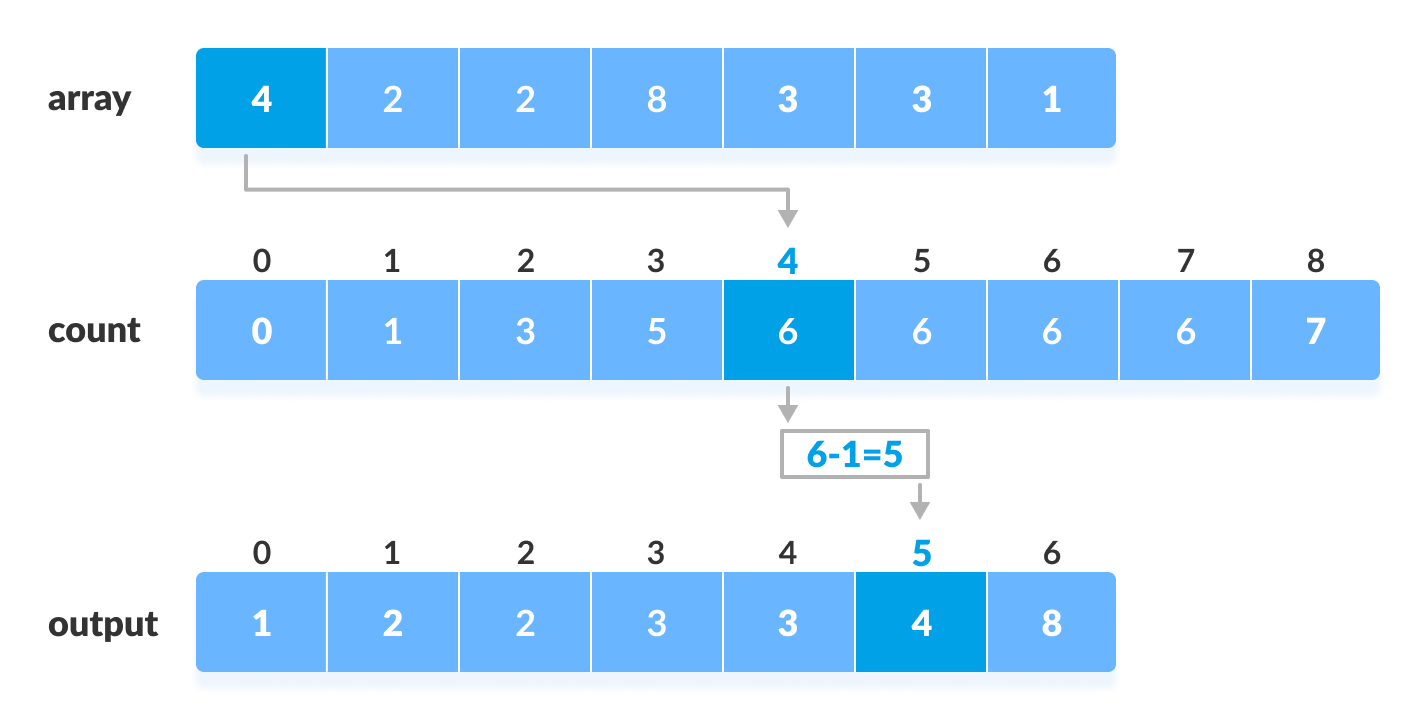
是一種用多一點的空間換取時間的方式，只能用來排序整數，總共需要3個array

  • A: Input unsorted array
  • B: Output sorted array
  • C: Working array

重點在利用C array就可以用$O(n+k)$的複雜度排序，先看A array的數字範圍，假設是[0,5]就開6個element的空間，並計算每一種A array的數字有幾個，例如0有3個、1有0個，接著累加C array，C[1]=C[0]+C[1], ，C[2]=C[0]+C[1]+C[2],…，以此類推，接著實際排序，排序方式非常簡單，從A array最後一個element看回來當作C array的index，直接對照key是多少，就把該數字排在B array對應的地方，接著C array該index的key減一

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
 
COUNTING-SORT(A,B,k)
// 初始化working array
for i=1 to k
    C[i] = 0
for j=1 to A.length
    C[A[j]]=C[A[j]]+1

// 累加working array
for i=2 to k
    C[i]=C[i]+C[i-1]

// 實際排序
for j=A.length downto 1
    B[C[A[j]]]=A[j]
    C[A[j]]=C[A[j]]-1

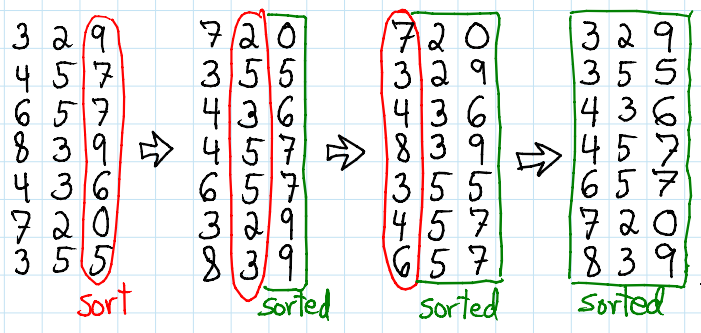
Radix Sort

專門用來排序相同位數的數字，從個位數開始排，很不直觀，原因是人從高位數開始排時，會自動分類以利之後再排，假設目前有5組數字，其中2個的高位數是4，此時人類會下意識把這兩個數字當成一組，再往低一位的數字比較，而不是所有數字一起比較，但這樣其實就是divide-and-conquer的演算法，並沒有比較特別

1
2
3
 
RADIX-SORT(A,d)
for i=1 to d
    Use a stable sorter to sort array A on digit i

Bucket Sort

想法就是像個籃子一樣，把同類型的丟進去，專門用來分類[0,1)的小數，可以用linked-list的結構實現

1
2
3
4
5
6
7
8
9
10
11
12
13
 
BUCKET-SORT(A)
// 初始化
n = A.length
Let B[0...n-1] be a new array // 有多少element就要有多少bucket
for i = 0 to n-1
    Make B[i] an empty list
for i = 1 to n
    INSERT A[i] into list B[⌊nA[i]⌋]

// 實際排序用看起來最慢的InsertionSort
for i = 0 to n-1
    Sort list B[i] with InsertionSort
Concatenate the lists B[0],B[1],...,B[n-1] together in order