Algorithm-Tree

Posted on | Post modified | In |

Algorithm-Tree

這個章節主要在介紹binary-search-tree和紅黑樹的各種操作和演算法實作

Operation BST RBT
Search
Insert
Delete
Minimum
Maximum
Successor
Predecessor		 $O(h)$ $O(lgn)$

Binary Search Tree(BST)

和前面提到的heap結構不一樣

  • BST主要為了「快速搜尋任意值」
  • Heap：為了「快速拿到最大值或最小值」

規則：

  • 左子樹所有值 < 根
  • 右子樹所有值 > 根
  • 中序走訪會得到排序結果

Operation

都可以在$O(h)$的複雜度做到，$h$代表tree的高度

  • Search 
    1
    2
    3
    4
    5
    6
      Iteratie-Tree-Search(x,k) // x代表目前的點，k代表想找的value
  while x≠NIL and k≠x.key
      if k<x.key
          x = x.left
      else x = x.right
  return x
  • Minimum
  • Maximum
  • Predecessor(前一個)
  • Successor(後一個) 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
      Tree-Successor(x) // 只要考慮兩種情況

  // 第一種是root本身往右邊找最小的就是successor
  if x.right ≠ NIL
      return Tree-Minimum(x.right)

  // 第二種是children要往上找才能找到successor
  y = x.p
  while y ≠ NIL and x == y.right
      x = y
      y = y.p
  return y
  • Insert 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
      Tree-Insert(T,z) // z代表要插入的node。分兩種情況，第一種是  插在某個parent底下當作children；第二種是要插入的z本身就是root
  y = NIL
  x = T.root
  while x ≠ NIL
      y = x
      if z.key < x.key
          x = x.left
      else x = x.right
  z.p = y
  if y == NIL
      T.root = z // 屬於要插入的z本身就是Tree的第一個node

  // 以下兩個都是第一種情況，z已經是y的children只是要區分比y大還是小
  else if z.key < y.key
      y.left = z
  else y.right = z
  • Delete:分三種情況
    • node z沒有任何children: 直接刪除
    • node z有一個children: 把z的parent的children pointer改成z的children
    • node z有兩個children: 把z.right中最小的node取代z
    1
    2
    3
    4
    5
    6
    7
    8
      Transplant(T,u,v) // 用v node取代u node
  if u.p == NIL // 代表u已經是root了
      T.root = v
  else if u == u.p.left // u是child且比parent小
      u.p.left = v
  else u.p.right = v // u是child且比parent大
  if v ≠ NIL
      v.p = u.p

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
      Tree-Delete(T,z)
  if z.left==NIL // Case A: 只有一個右邊的child
      Transplant(T,z,z.right)
  else if z.right == NIL // Case B: 只有一個左邊的child
      Transplant(T,z,z.left)
  else
      y = Tree-Minimum(z.right)
      if y.p ≠ z // Case D: 有兩個children且可以直接用successor取代z
          Transplant(T,y,y.right)
          y.right = z.right
          y.right.p = y
      Transplant(T,z,y) // Case C,D: 有兩個children且successor就是z.right
      y.left = z.left
      y.left.p = y

Red-Black Trees

  • 可以保證tree的高度是$O(lgn)$
  • 有五個屬性
    1. 每一個node不是紅就是黑
    2. root一定是黑
    3. NIL一定是黑
    4. 如果一個node是紅色，該node的children一定是黑色
    5. 每一個node往下看leaf任意路徑所碰到的黑色node數量會是一樣的
  • 這些規則確保樹不會嚴重傾斜(balanced)
  • 最多只需要3次rotation就可以保持平衡

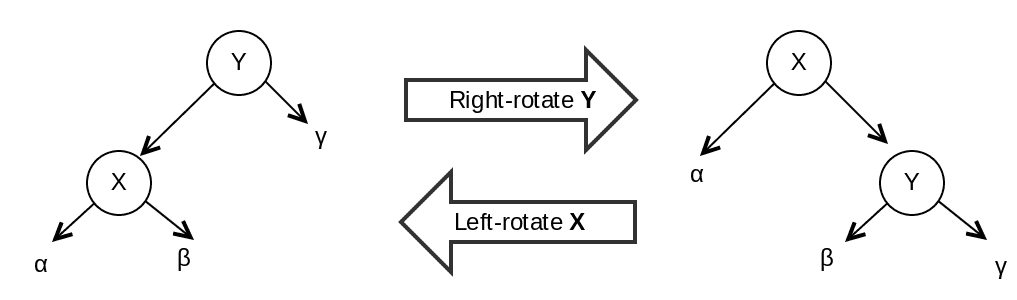
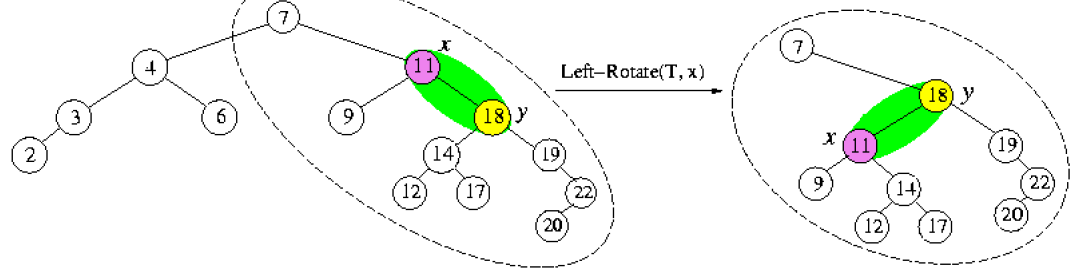
Rotation

只有分右轉或左轉，都不影響BST的特性，只會改變structure 

1
2
3
4
5
6
7
8
9
10
11
12
13
Left-Rotate(T,x)
y = x.right // Set y
x.right = y.left // Turn y's left subtree into x 's right subtree
if y.left ≠ T.nil
    y.left.p = x
y.p = x.p // Link x 's parent to y
if x.p == T.nil
    T.root = y
else if x == x.p.left // 代表x是left child
    x.p.left = y
else x.p.right = y
y.left = x // Put x on y 's left
x.p = y

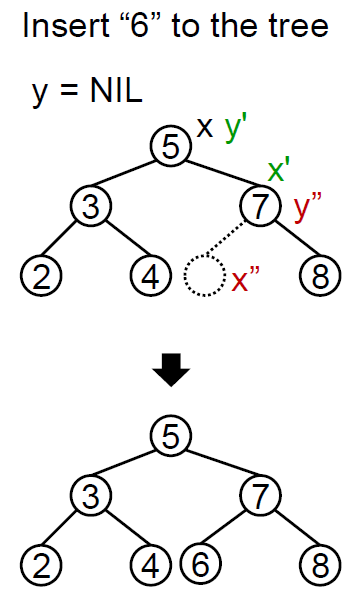
Insertion

  • RB-Insert 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
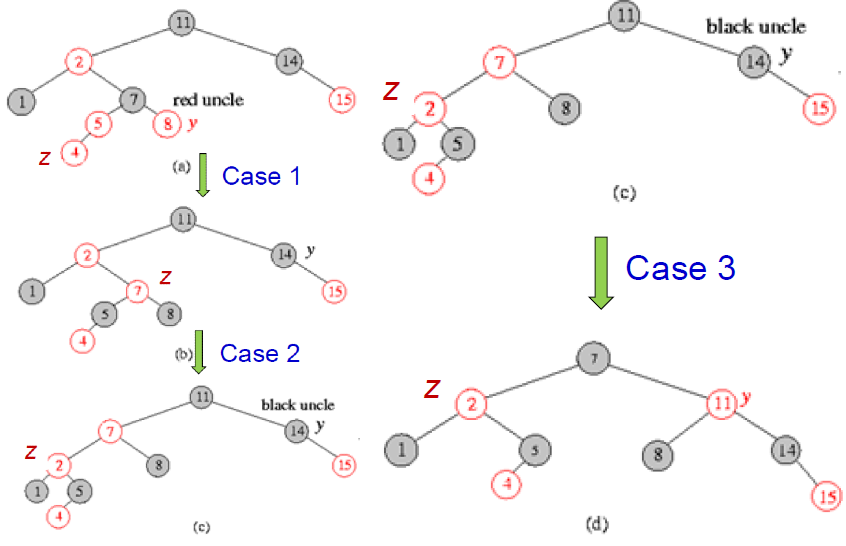
    21
      RB-Insert(T,z)
  y = T.nil
  x = T.root
  while x ≠ T.nil
      y = x
      if z.key < x.key
          x = x.left
      else x = x.right
  z.p = y
  if y == T.nil
      T.root = z
  elseif z.key < y.key
      y.left = z
  else y.right = z

  /*---以上部分都和Tree-Insert一樣---*/

  z.left = T.nil
  z.right = T.nil
  z.color = RED
  RB-Insert-Fixup(T.z)
  • RB-Insert-Fixup 基本上就是一邊看課本範例一邊對照pseudo code的case，就大概知道邏輯怎麼跑，但要說他的case是基於什麼pattern，我沒有寫筆記，代表上課時也沒有特別講 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
      RB-Insert-Fixup(T, z)
  while z.p.color == RED
      if z.p == z.p.p.left
          y = z.p.p.right
          if y.color == RED
              z.p.color = BLACK   // case 1
              y.color = BLACK     // case 1
              z.p.p.color = RED   // case 1
              z = z.p.p           // case 1
          else
              if z == z.p.right
                  z = z.p             // case 2
                  Left-Rotate(T, z)   // case 2
              z.p.color = BLACK           // case 3
              z.p.p.color = RED           // case 3
              Right-Rotate(T, z.p.p)      // case 3
      else (same as then clause with "right" and "left" exchanged)
  T.root.color = BLACK

Delete

  • z有一個chile 
    1
    2
    3
    4
    5
    6
    7
    8
      /*---和Tree-Transplant幾乎一樣---*/
  RB-Transplant(T , u, v)
  if u.p == T.nil
      T.root = v
  elseif u == u.p.left
      u.p.left = v
  else u.p.right = v
      v.p = u.p
  • z有兩個children 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
      RB-Delete(T ,z)
  y = z
  y-original-color = y.color
  if z.left == T.nil // case A
      x = z.right
      RB-Transplant(T, z, z.right)
  elseif z.right == T.nil // case B
      x = z.left
      RB-Transplant(T, z, z.left)
  else y = Tree-Minimum(z.right)
      y-original-color = y.color
      x = y.right
      if y.p == z // case C
          x.p = y
      else RB-Transplant(T, y, y.right)
          y.right = z.right // case D
          y.right.p = y
      Transplant(T, z, y) // cases C, D
      y.left = z.left
      y.left.p = y
      y.color = z.color
  if y original color == BLACK
      RB-Delete-Fixup(T, x)

Deleteion-Color-Fixup

以下的case前提是x是x.p的left child

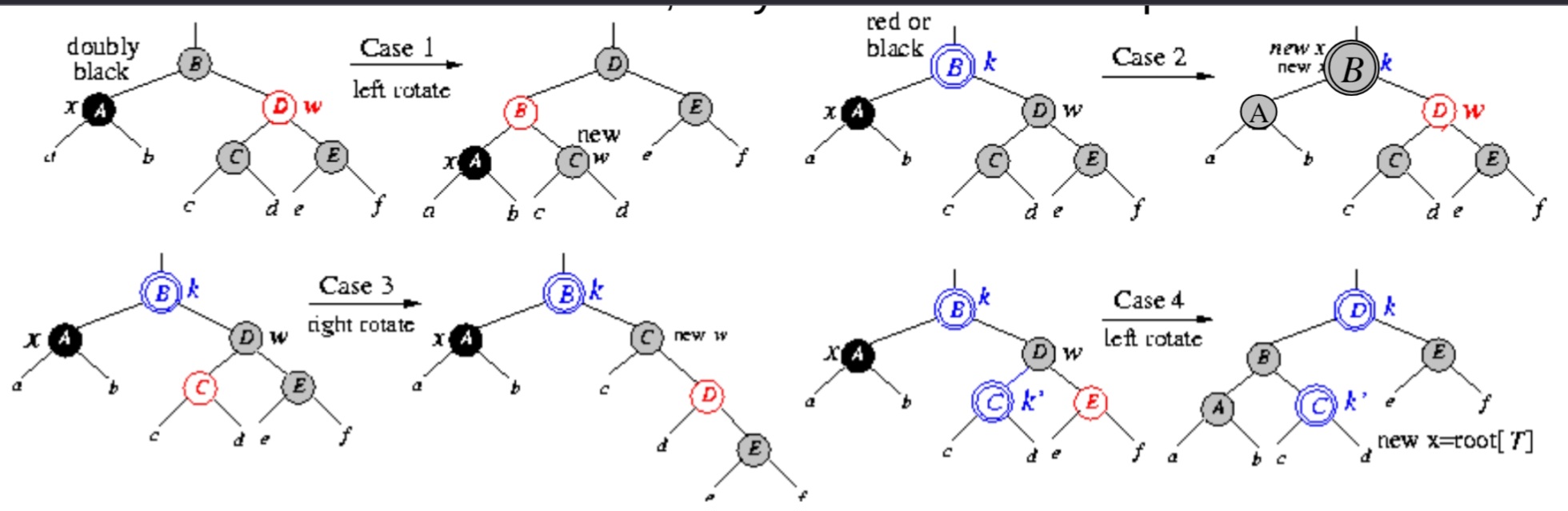
  1. Case 1: The doubly black node x has a red sibling w. 2.Case 2: x has a black sibling and two black nephews.
  2. Case 3: x has a black sibling, and its left nephew is red and its right nephew is black.
  3. Case 4: x has a black sibling, and its right nephew is red (left nephew can be any color).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
RB-Delete-Fixup(T,x)
while x ≠ T.root and x.color == BLACK
    if x == x.p.left
        w = x.p.right
        if w.color == RED
            w.color = BLACK     // Case 1
            x.p.color = RED       // Case 1
            Left-Rotate(T, x.p)  // Case 1
            w = x.p.right            // Case 1
        If w.left.color == BLACK and w.right.color == BLACK
            w.color = RED // Case 2
            x = x.p             // Case 2
        else if w.right.color == BLACK
            w.left.color = BLACK // Case 3
            w.color = RED             // Case 3
            Right-Rotate(T, w)      // Case 3
            w = x.p.right                // Case 3
            w.color = x.p.color        // Case 4
            x.p.color = BLACK        // Case 4
            w.right.color = BLACK // Case 4
            Left-Rotate(T, x.p)        // Case 4
            x = T.root
    else (same as then clause with "right" and "left" exchanged)
x.color = BLACK