Algorithm-Graphs

Posted on | Post modified | In |

Algorithm-Graphs

Terminology

  • Graph: 包含$G(V,E)$點到集合$V$ vertices(node)，和有向/無向邊的集合edge $E$，任何binary之間的關係就是Graph(不論有無連結)
  • Adjacency List: 是一種紀錄graph上點之間的關係的一種資料結構，詳細可以看資料結構筆記

Elementary Graph Algorithms

Breadth-First Search(BFS)

下面pseudo code的目的是給一個graph和起始的點s，計算出圖上各個點與s之間的距離

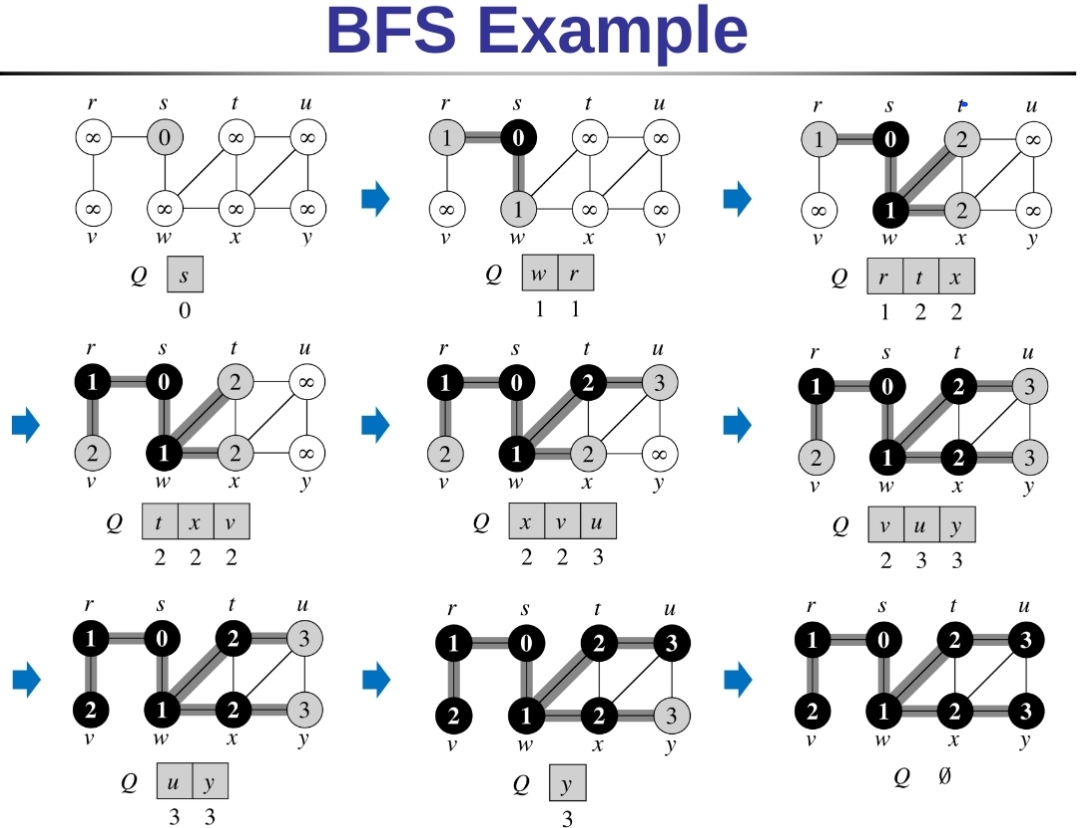
  • u.d: 代表和起始點s之間的距離
  • u.pi: 代表u的上一個
  • 利用Queue處理才會有BFS的效果
  • Time: $O(V+E)$(Adjacency List)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
 
BFS(G,s)
// 初始化，全部都是白色且無限大的距離，s本身是灰色且距離是零
for each vertex u inG.V - {s}
    u.color = WHITE // 代表undiscovered
    u.d = ∞
    u.pi = NIL
s.color = GRAY // 代表discovered
s.d = 0
s.pi = NIL
Q = Ø
Enqueue(Q, s)

// 正是計算各點與s的距離
while Q ≠ Ø
    u = Dequeue[Q]
    for each vertex v in G.Adj[u]
        if v.color == WHITE
            v.color = GRAY
            v.d = u.d + 1
            v.pi = u
            Enqueue(Q,v)
    u.color = BLACK // 代表edge的鄰居也被discovered

Depth-First Search(DFS)

  • u.color: 和BFS定義的一樣，分為WHITE, GRAY, BLACK
  • u.d: discovery time
  • u.f: finishing time
  • u.pi: u的predecessor
  • Time: $O(V+E)$(adjacency list)

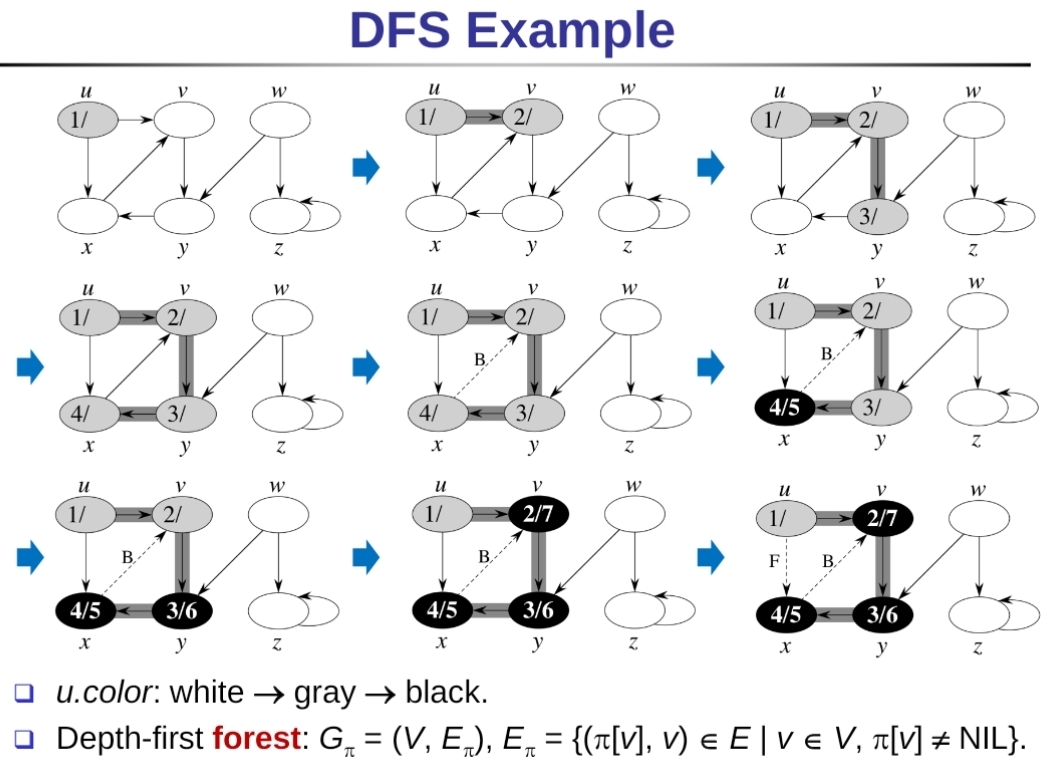範例中vertex的兩個數字分別代表u.d/u.f，另外，由於分析到x的地方會跳出recursive loop，則time要再加一

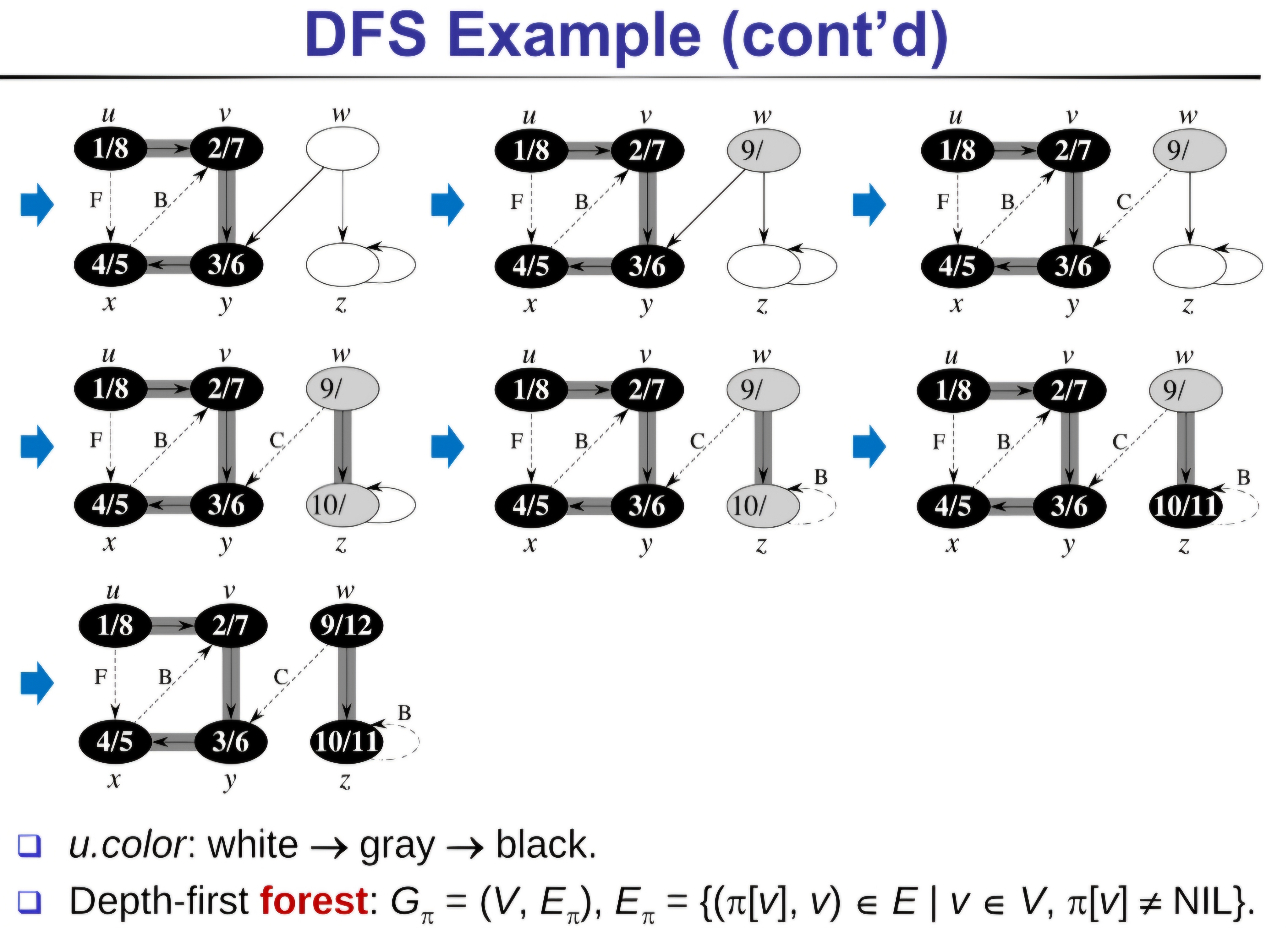等到左半邊都分析完了，就會直接跳到w

1
2
3
4
5
6
7
8
9
10
11
 
DFS(G)
// 初始化graph
for each vertex u  G.V
    u.color = WHITE
    u.pi = NIL
time = 0

// 實際判斷距離
for each vertex u  G.V
    if u.color == WHITE
        DFS-Visit(G, u)

1
2
3
4
5
6
7
8
9
10
11
 
DFS-Visit(G, u)
time = time + 1 // white vertex u has just been discovered
u.d = time
u.color = GRAY
for each vertex v  G.Adj[u] // Explore edge (u,v)
    if v.color == WHITE
        v.pi = u
        DFS-Visit(G, v) // 要用recursive的方法才會有DFS的效果
u.color = BLACK // Blacken u; it is finished
time = time +1
u.f = time

BFS應用-Lee’s Maze Router

  • 可以用在IC佈線上: 利用wave propagation的方式，找一個從點S到點T的路徑(在單層single-layer的情況下)
  • 優點: 只要路徑存在就一定找的到最快的path
  • 缺點: 要是unweighted，且時間和空間複雜度為$O(MN)$太大(在$M\times N$的grid上)

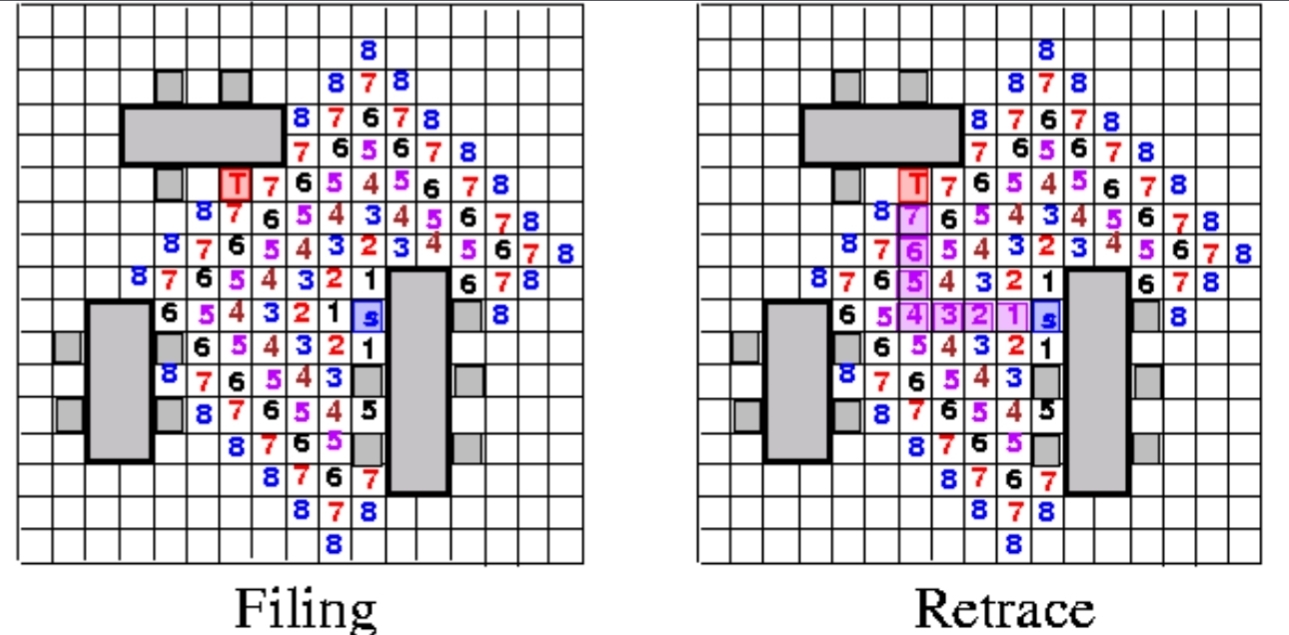
BFS+DFS應用-Soukup’s Maze Router

同樣是找點S到點T的path，好處是雖然時間和空間的複雜度和Lee’s一樣但卻比前者快10-15倍，不過路徑不一定是最短的

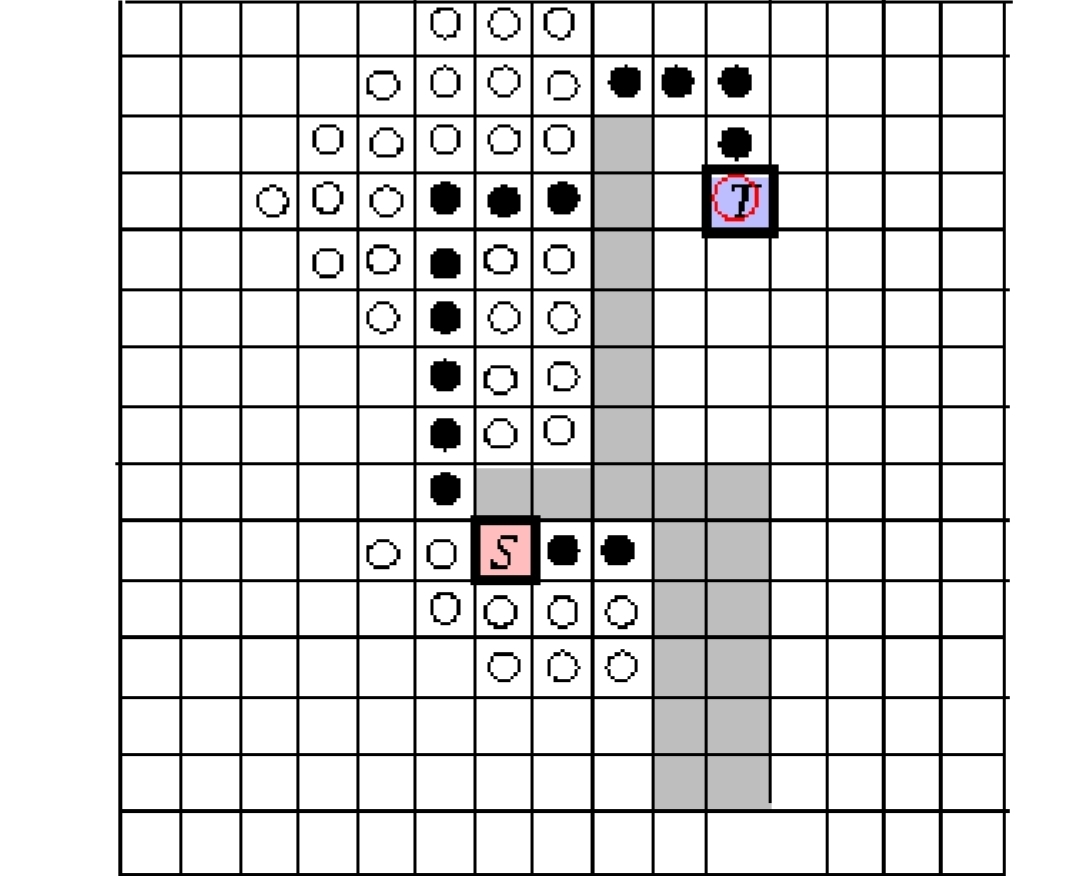
  • 黑色圓是DFS
  • 白色圓是BFS
  1. 先看S和T的直線
  2. 撞到障礙物就變成黑點
  3. 以黑點為原點重新計算距離，直到有一點比黑點更接近T再繼續衝

Topological Sort

很簡單，是一種對有向無環圖(directed acyclic graph, DAG)的排序方式，把所有頂點排成一個線性順序，使得每一條邊$u\to v$，u 都排在 v 前面。👉 有「先後關係」的排序。

  • Time: $O(V+E)$(adjacency list)
1
2
3
4
 
Topological-Sort(G)
call DFS(G) to compute finishing times v.f for each vertex v
as each vertex is finished, insert it onto the front of a linked list
return the linked list of vertices

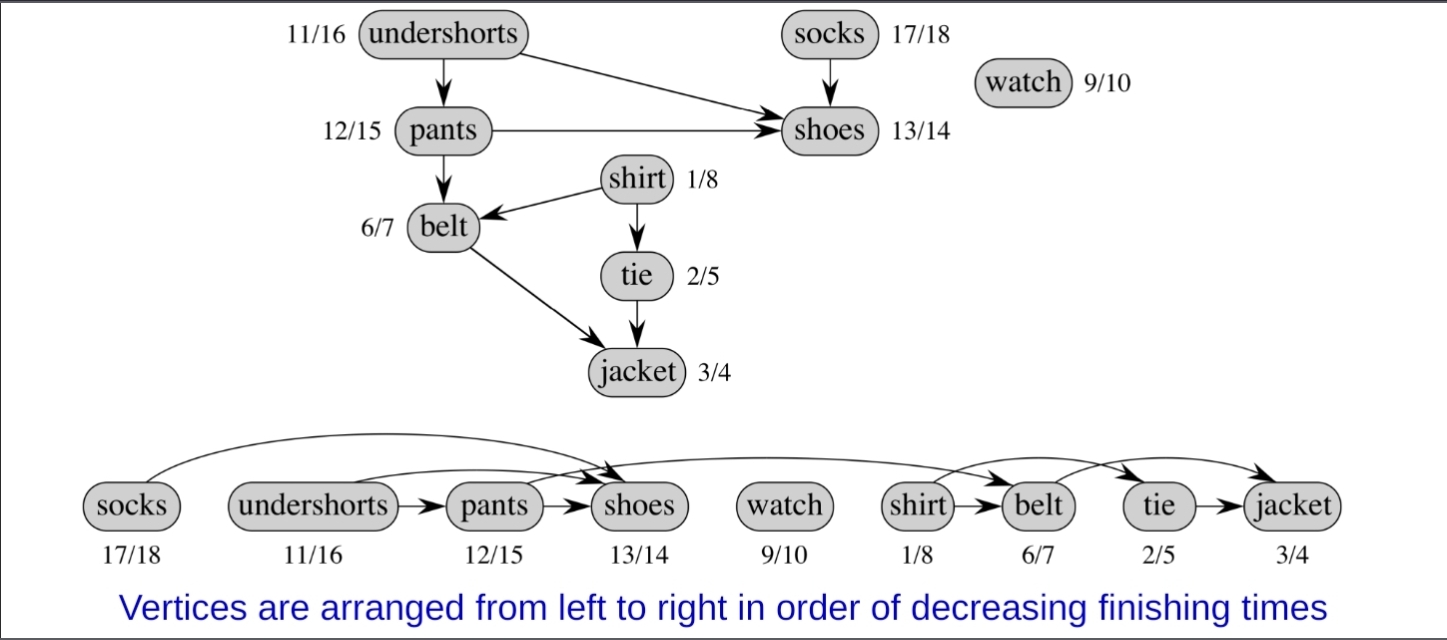
其實就是一路往右排序，每一個task的兩個數字分別代表start time/finish time，結束時間比較早的往右排

Strongly Connected Component(SCC)

是有向圖中的一個重要概念，在有向圖中，一個頂點集合 $C$，任兩個點 $u,v\in C$ 都滿足$u\to v$ 且 $v\to u$ 都走得到，則 $C$ 是一個 Strongly Connected Component。👉 彼此「來得去、去得回」

  • 比較 |類型|適用圖|條件| |—|—|—| |Connected Component|無向圖|走得到就算| |Strongly Connected Component|有向圖|來回都走得到|
1
2
3
4
5
6
 
// 先找誰最後離開圖，再反過來走一次
Strongly-Connected-Components(G)
call DFS(G) to compute finishing times u.f for each vertex u // 利用DFS找出圖上的vertices 的finish time(u.f)
compute G_Transpose // 把圖反向
call DFS(G_Transpose), but in the main loop of DFS, consider the vertices in order of decreasing u.f (as computed in line 1) // 從最後一個推回來
output the vertices of each tree in the depth-first forest of step 3 as a separate strongly connected component
  • $G^T=(V,E^T)$: G的Transpose，$E^T={(u,v):(v,u)\in E}
  • Time: $O(V+E)$(adjacency list)

Minimum Spanning Trees(MST)

  • Spanning Tree(生成樹): 用 $V-1$ 條邊連通所有 $V$ 個頂點且無 cycle
  • Edge Count: $\mid E_{MST}\mid = V-1$
  • Cut Property(切割性質): 對任意切割$(S,V-S)$(其實就是分成兩個群)，跨越該 cut 的最小權重邊，一定存在於某棵 MST 中
    • Crossing edge：跨越 cut 的邊
    • Light edge：跨越該 cut 的最小權重邊

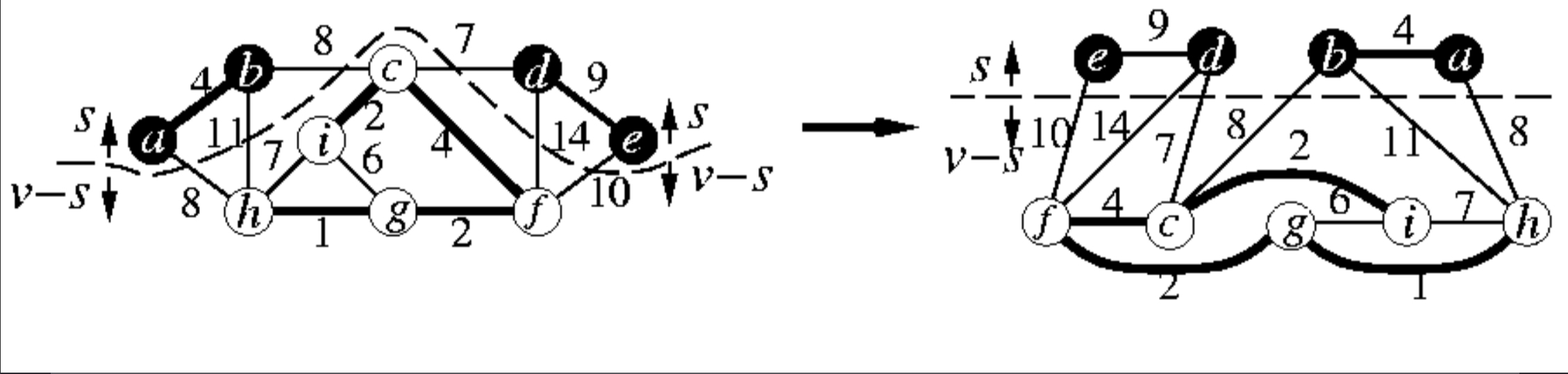
    • 有被虛線切到的就是cut edge
  • Input: 無向的graph $G=(V,E)$，有權重的edge
  • Objective: 目的是找到能夠連結所有vertices但又最短的path
  • 應用
    • circuit interconnection(minimizing tree radius): 連接所有 pin，線長 ≈ 成本 👉 先用 MST 降低總線長，再做優化
    • communication network(minimize tree diameter): 城市要鋪光纖、公司內部拉網路、水管、電線、油管，節點是地點，邊等於鋪設成本 👉 MST = 最便宜的整體鋪設方案
1
2
3
4
5
6
 
Generic-MST(G,w)
A = ∅
while A does not form a spanning tree
    find an edge (u,v) that is safe for A
    A = A ∪ {(u,v)}
return A

實作

||Kruskal|Prim| |—|—|—| |觀點|邊|點| |資料結構|Union-Find|Priority Queue| |適合|稀疏圖|稠密圖| |是否需要連通|否（變森林）|是|

Kruskal’s

  • 用Disjoint set forest處理，也是一種Greedy演算法
  • Time: $O(ElgE+V)$
  1. 由小到大排序，所有「邊(Edge)」的權重(Weigh)。
  2. 從小到大開始取那些「邊(Edge)」，前提是取到的Edge不能形成一個迴圈(loop, cycle)。要檢查
  3. 重複步驟 2的動作，直到最後已經不能再取。

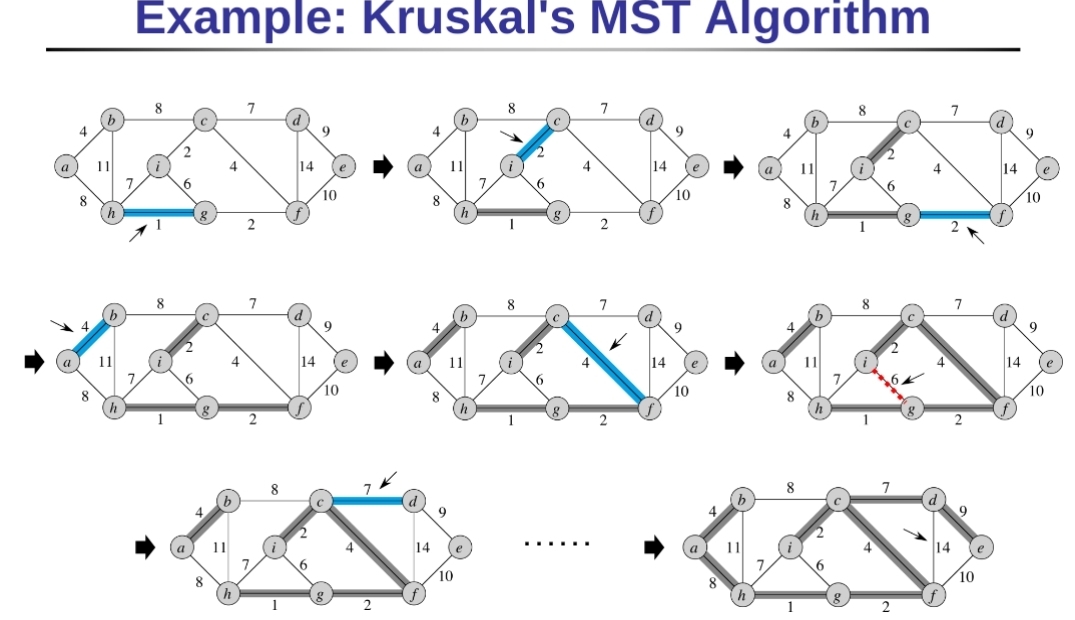
$(i,g)$之間的6沒有被算入是因為產生了cycle，另一個說法是這個edge本身不是一個合法的cut edge，也就是切到$(i,g)$但又不切到其他已經選到的edge

1
2
3
4
5
6
7
8
9
10
 
MST-Kruskal(G,w)
A = Ø
for each vertex v in G.V // O(V)
    Make-Set(v)
sort the edges of G.E by nondecreasing weight w // 由小到大排序 > O(ElgE)
for each edge (u,v) in G.E, in order by nondecreasing weight // 從weight最低的開始 > O(E) > 最worst的狀況是所有edge都要檢查一次
    if Find-Set(u) ≠ Find-Set(v) // 其實就是檢查有沒有cycle，因為如果有cycle那就一定找的到同一個representative
        A = A  {(u, v)}
        Union(u,v)
return A

Prim’s

  • Time
    • 用Binary Heap: $O(ElV)$
    • 用Fibonacci Heap: $O(E+VlgV)$
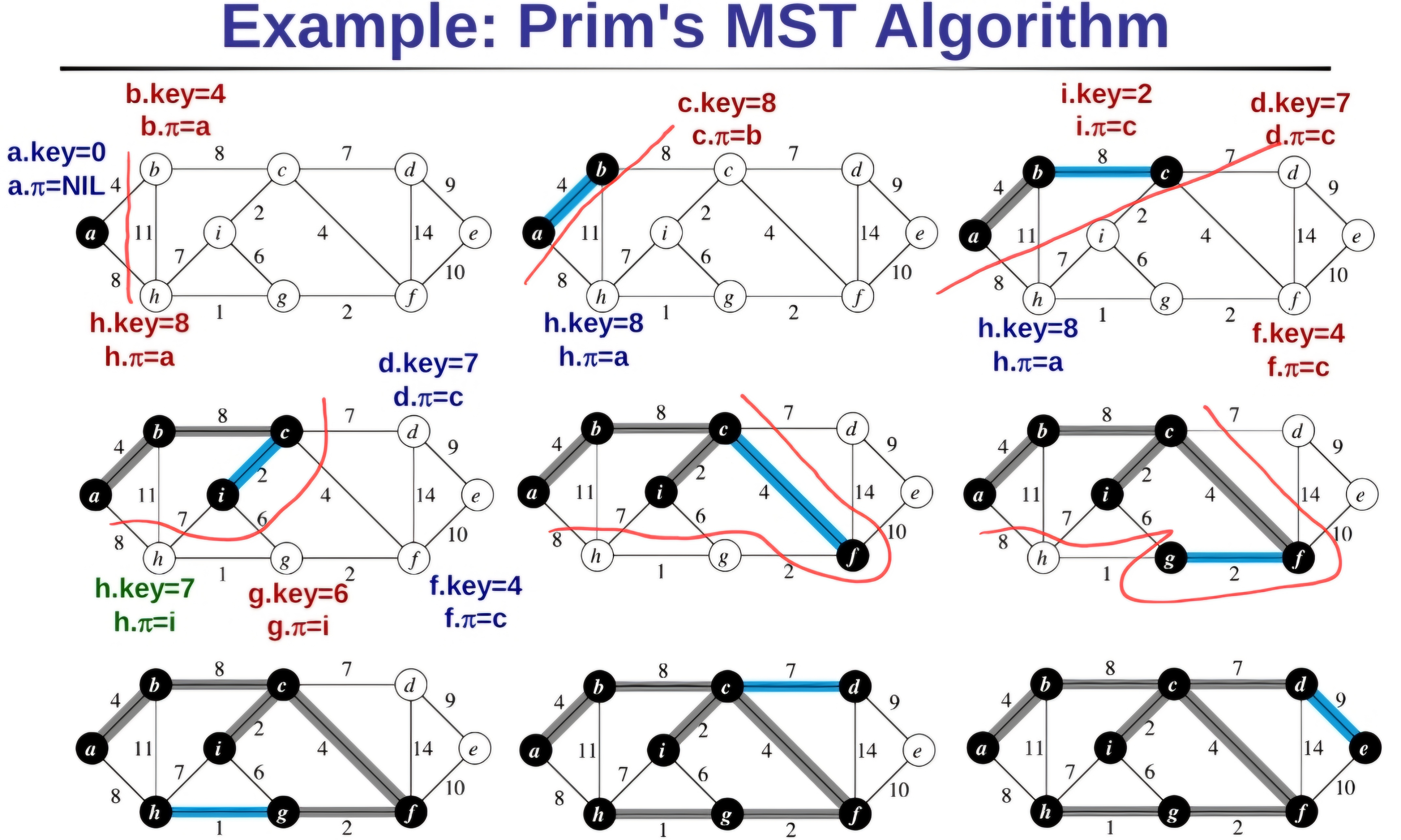
  1. 初始化：首先，選擇一個起始節點，將其視為MST的一部分，同時初始化一個空的MST。
  2. 找到最小邊：在已經選中的節點和未選中的節點之間，選擇一條權重最小的邊，並將其添加到最小生成樹中。這個邊的一個端點必須是已選中的節點，另一個端點必須是未選中的節點。
  3. 重複步驟2：持續執行步驟2，直到最小生成樹包含了所有節點。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
 
MST-Prim(G,w,r)
// Q: priority queue for vertices not in the tree, based on key.
// key: min weight of any edge connecting to a vertex in the tree.

// 初始化 > O(V)
for each vertex u in G.V
    u.key = ∞
    u.pi = NIL
r.key = 0
Q = G.V

// 真正開始處理MST
while Q ≠ ∅ // O(VlgV)
    u = Extract-Min(Q) // 用Binary Heap > O(lgV)
    for each vertex v in G.Adj[u] // O(E)
        if v in Q and w(u,v) < v.key // 找weight最小的鄰邊
            v.pi = u
            v.key = w(u,v)

Shortest Paths

Single Source Shortest Path(SSSP)

  • Input: 有向圖$G(V,E)$且含weighted edge以及一個指定的出發點$s$
    • Weight of Path: $p=<v_0,v_1,…,v_k>$: $w(p)=\sum_{i=1}^kw(v_{i-1},v_i)$
    • Weight Function: $w:E\to \mathbb{R}$
  • Objective: 找到一條從$s$出發連到其他所有點的最小weight的路徑 \(\delta(u,v)=\left\{ \begin{array}{l} \min\{w(p):u\xrightarrow{p}v\}\ \text{if there is a path from}\ u\ \text{to}\ v \\ \infty\ \text{otherwise} \end{array} \right.\)
  • 應用: weight可以是任何東西，例如距離、時間、電線成本、delay等等

All Pairs Shortest Paths(APSP)

Maximum Flow