Algorithm-Greedy Algorithm

Posted on | Post modified | In |

Algorithm-Greedy Algorithm

  • 總是會做出當下看起來最佳的選擇
  • 和Heuristic(經驗法則)的差別是Greedy Algorithm可以找到最佳解
  • Vortex Cover的例子可以直接看講義

什麼時候適合用Greedy Algorithm

  • 問題有 Greedy-choice property 也就是當「每一步做當下最好的選擇」不會影響未來最優解時，就可以用 Greedy，DP需要檢查subproblem的solution
  • 且通常有 optimal substructure

和DP的差異

其實就是greedy-choice property，如果greedy solution不是optimal就可以考慮用DP

Activity-Selection Problem(排程問題)

想像成CPU的工作

  • Input:
    • $S={1,2,…,n}$ activity的集合
    • 該集合包含activity $i$的開始時間$s_i$和結束時間$f_i$
  • Objective: 在一個人（或資源）一次只能做一個活動且兩個活動不重疊才能同時被選的條件下，選出最多個彼此不衝突的活動

用Greedy的方式解

  1. 先排序結束時間$f_i$，由小到大
  2. 選擇第一個activity
  3. 往下選，只要下一個activity的$s_i\le f_j$就選，$j$代表最近選擇的activity
1
2
3
4
5
6
7
8
9
10
 
Greedy-Activity-Selector(s,f)
// Assume f1≤f2≤…≤fn.
n = s.length
A = {1}
j = 1
for i = 2 to n
    if s[i] ≥ f[j]
        A = A ⋃ {i}
        j = i
return A
  • Time Complexity: $O(n)$(不包含sorting)，有包含的話是$O(nlgn)$
  • Optimality Proofs的部分可以直接參考講義，有點複雜，總而言之

    如果不選最早結束的活動，而選一個結束較晚的，那只會減少後面可選活動的空間，因此不可能更好

Knapsack Problem

  • Input: $n$個item；$\vec{v}$代表各個item的價值；$\vec{w}$代表各個item的重量；$W$代表背包容量
  • Objective: 裝越有價值的東西越好

0-1 Knapsack Problem

  • 只有拿或不拿兩個選項
  • 網路上有code
  • Time: 如果用DP的方式解，會是$O(nW)$, $n$代表有幾個物件, $W$是指背包載重。不是polynomial time，因為$W$不是input size(就是可以用個數的東西，例如珠寶)，會被歸類在NP-Complete

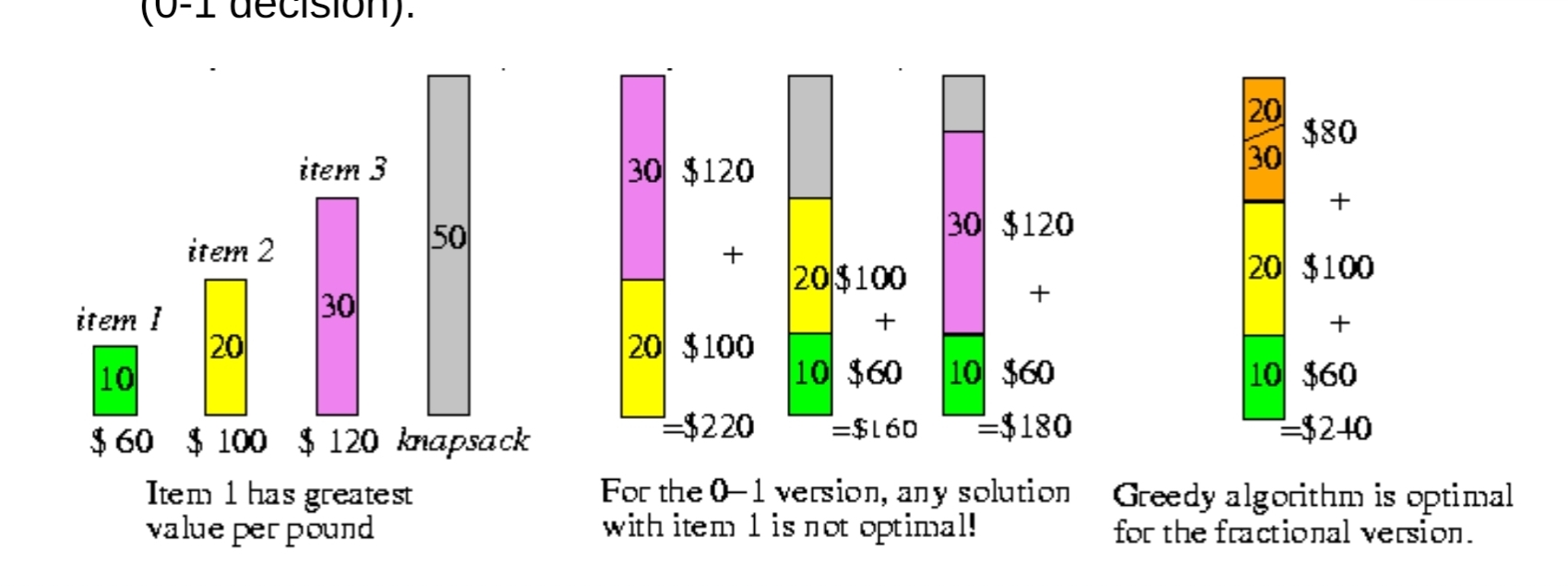
Fractional Knapsack Problem

  • 代表可以拿一部分
  • 用Greedy的方式就是先拿走單位價值高的
  • 先算出每個item的單位價值，並盡可能的全部拿，剩下的就拿一部分就好

Huffman Codes

  • Coding(編碼)用途：data compression, instruction-set encoding, etc.
  • Objective: 讓編碼後的cost最小化
    • 如何定義cost: frequency * depth
    \[B(T)=\sum\limits_{c\in C}c.freq\cdots d_T(c)\]
  • Binary character code: 用{0,1}組成獨一無二的code表示字母
    • Fixed-length code: 每一個字母的編碼長度都相同
    • Variable-lengh code: 編碼的長度根據字母出現的頻率而定
    • 每100個character的cost，Variable-length code的cost比較小

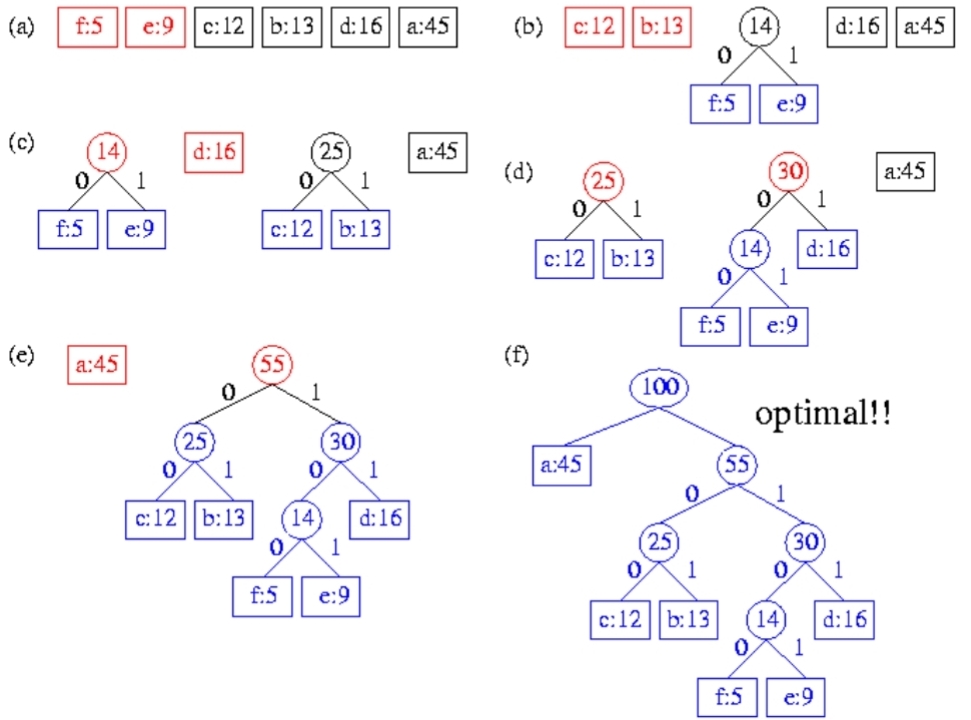
如何用Greedy解-Huffman’s Algorithm

，核心概念是越常出現的字母，深度要越淺，所以要給每個字母的出現頻率

  1. 先把每個字母的頻率排序由小到大
  2. 把最小的兩個合起來當作一個node再排序一次
  3. 重複步驟1,2直到建完一顆binary heap

  • Time: $O(nlgn)$ 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    		 
      Huffman(C)
  n = |C|
  Q = C // Q: a min-priority queue (a min heap) O(nlgn)建binary heap
  for i = 1 to n -1
      Allocate a new node z
      z.left = x = Extract-Min(Q) // O(lgn)
      z.right = y = Extract-Min(Q) // O(lgn)
      z.freq = x.freq + y.freq
      Insert(Q, z) // O(lgn)
  return Extract-Min(Q) //return the root of the tree

    確認是否符合兩個條件

  • Greedy Choice Property: 如果以上方法不是最佳解，那麼就把tree上任意node互換，cost有無比較低，如果沒有就代表目前的版本已經是optimal
  • Optimal Substructure: 複雜，看課本

Task Scheduling

  • Objective: 每一個task需要的時間都相同，但是會有自己的dwadline，沒有在deadline之前做完，會有penalty
  • Input:
    • $n$個task$S={1,2,…,n}$
    • Deadline: $d_1,d_2,…,d_n$
    • Penalties: $w_1,w_2,…,w_n$
  • $A$代表任務的集合
  • $N_t(A)$代表在$A$集合中的task，小於等於$t$這個時間點的task有幾個

  1. 先排序penalty，有小到大

    Task 1 2 3 4 5 6 7
    $d_i$ 4 2 4 3 1 4 6
    $w_i$ 70 60 50 40 30 20 10

  2. 按照下表，指到Task $n$就讓$N_t(A) += 1\mid n≤t$，要判斷加完之後是否符合$N_t(A)≤t$，如果超過就流標，代表這個Task無法在時間內處理完，就要放棄這個Task並接受penalty

    指到 Task 1 Task 2 Task 3 Task 4 Task 5 Task 6 Task 7
    $N_1(A)$ 0 0 0 0 1>0 0 0
    $N_2(A)$ 0 1 1 1 2>1 1 1
    $N_3(A)$ 0 1 1 2 3>2 3>2 2
    $N_4(A)$ 1 2 3 4 5>4 5>4 4
    $N_5(A)$ 1 2 3 4 5>4 5>4 4
    $N_6(A)$ 1 2 3 4 5>4 5>4 5

  3. 依照前面的統計結果指到Task 5,6的時候流標，代表最終能夠完成的只有TASK 1,2,3,4,7，按照deadline排序如下，如果deadline一樣就隨便排

    • Optimal Scheduling: 2,4,1,3,7,5,6
    • Penalty: 30+20=50